Regressão linear no machine learning, que que é isso?

Regressão linear no machine learning, que que é isso? Confira este post e entenda os fundamentos matemáticos por trás das previsões de IA.

O que diabos é regressão linear?

Machine Learning é um ramo da Inteligência Artificial para o desenvolvimento de algoritmos e modelos estatísticos que podem aprender a partir de dados e fazer previsões.

A regressão linear é um tipo de algoritmo de machine learning (algoritmo de aprendizado supervisionado) que aprende a partir de conjuntos de dados rotulados.

Depois, a regressão mapeia os pontos de dados para as funções lineares mais otimizadas que podem ser usadas para previsões em novos conjuntos de dados.

Primeiro, precisamos entender o que é aprendizado supervisionado.

É um tipo de aprendizado de máquina onde o algoritmo aprende a partir de dados rotulados.

Dados rotulados significam que o valor alvo respectivo do conjunto de dados já é conhecido.

O aprendizado supervisionado tem dois tipos principais: classificação e regressão.

Classificação

Prediz a classe do conjunto de dados com base na variável de entrada independente.

Classes são os valores categóricos ou discretos.

Como, por exemplo, se a imagem de um animal é de um gato ou de um cachorro?

Até um bebê novinho consegue diferenciar um gato de um cachorro.

Regressão

Prediz variáveis contínuas de saída com base na variável de entrada independente.

Por exemplo, a previsão de preços de casas com base em diferentes parâmetros, como a idade da casa, distância da estrada principal, localização, área, etc.

Quem não quer saber o preço exato da casa dos seus sonhos com base em um monte de números?

Agora, vamos discutir um dos tipos mais simples de regressão, a Regressão Linear.

Prepare-se para o “emocionante” no mundo das linhas retas!

Ok, mas o que é aprendizado supervisionado?

Imagine que você está ensinando um papagaio a falar.

Você mostra para ele uma maçã e diz “maçã”.

Isso é um dado rotulado.

Você já sabe que é uma maçã e está tentando ensinar o papagaio (ou algoritmo) a reconhecer e repetir isso.

No aprendizado supervisionado, fazemos algo parecido com os nossos algoritmos.

Damos aos algoritmos dados rotulados e pedimos para eles aprenderem as relações.

Classificação vs. Regressão

Vamos entender de forma mais boba como isso funciona.

Classificação (aprendizado supervisionado)

É como se o algoritmo estivesse jogando “Adivinha quem é?”

Ele tem que classificar os dados em categorias específicas.

Por exemplo, “Essa imagem é um gato ou um cachorro?”

Algo super útil para os milhões de vídeos de gatinhos na internet, não é?

Regressão (aprendizado supervisionado)

É como prever quanto tempo você vai ficar preso no trânsito com base na distância, hora do dia e seu azar natural.

É contínuo e tenta prever um valor.

Tipo, “Qual será o preço dessa casa no mercado imobiliário superinflacionado?”

Regressão Linear: a musa das linhas retas

Finalmente, chegamos à regressão linear.

A ideia aqui é simples: traçar uma linha reta que melhor se ajuste a todos os pontos de dados.

Pense nisso como tentar traçar a linha perfeita no gráfico para que você possa prever futuros pontos de dados.

Na prática, é como tentar prever se você vai precisar de mais café para sobreviver ao dia com base nas horas de sono que teve.

Então, da próxima vez que você ouvir sobre a “magia” da regressão linear no machine learning, lembre-se…

É só uma linha reta tentando fazer sentido no caos dos dados.

E, claro, sempre podemos confiar na simplicidade de uma linha reta para resolver nossos problemas complexos, certo?

Os vários tipos de regressão linear

Regressão linear é um tipo de algoritmo de aprendizado supervisionado que calcula a relação linear entre a variável dependente e uma ou mais características independentes.

E depois cria uma equação linear para se ajustar aos dados observados.

Quando há apenas uma característica independente, chamamos de Regressão Linear Simples.

Se houver mais de uma característica, então é a Regressão Linear Múltipla.

Da mesma forma, quando há apenas uma variável dependente, temos a Regressão Linear Univariada.

Se houver mais de uma variável dependente, trata-se da Regressão Multivariada.

Mas por quê raios a regressão linear é tão relevante?

A interpretabilidade da regressão linear é top.

A equação do modelo de regressão linear dá coeficientes claros que mostram o impacto de cada variável independente na variável dependente.

Isso facilita muito a compreensão das dinâmicas subjacentes.

A regressão linear é transparente, fácil de implementar e serve como base para algoritmos mais complexos.

A regressão linear não é apenas uma ferramenta de previsão.

Ela forma a base para vários modelos avançados.

Técnicas como regularização e máquinas de vetor de suporte começaram na regressão linear…

Além disso, a regressão linear serve para testes de hipóteses.

Isso permite que os pesquisadores validem suas premissas chave sobre os dados.

Regressão linear simples

Esta é a forma mais simples de regressão linear.

Ela usa apenas uma variável independente e uma variável dependente.

A equação para regressão linear simples é:

y = β0​ + β1​X

Onde:

• Y é a variável dependente
• X é a variável independente
• β0 é o intercepto
• β1​ é o coeficiente angular

Regressão linear múltipla

Esta envolve mais de uma variável independente e uma variável dependente.

A equação para regressão linear múltipla é:

y = β0​ + β1​X1​ + β2​X2 ​+ ⋯ + βn​Xn​

Onde:

• Y é a variável dependente
• X1, X2, … , Xn são as variáveis independentes
• β0 é o intercepto
• β1, β2, … , βn são os coeficientes angulares

O objetivo do algoritmo é encontrar a melhor equação de linha de ajuste que possa prever os valores com base nas variáveis independentes.

Em um conjunto de regressão, temos registros com valores X e Y e esses valores servem para aprender uma função.

Se você quiser prever Y a partir de um X desconhecido, você pode usar essa função aprendida.

Na regressão, precisamos encontrar o valor de Y.

Então é necessária uma função que preveja um Y contínuo no caso de regressão, dados vários X como características independentes.

Qual é o grande produto da regressão linear?

Então, aí está a mágica da regressão linear, a técnica milagrosa que transforma números em previsões brilhantes!

Claro, desde que você consiga se lembrar de todos esses βs e Xs e não se perca no meio do caminho.

Afinal, quem precisa de complexidade quando você pode só traçar uma linha reta e esperar que tudo dê certo, não é mesmo?

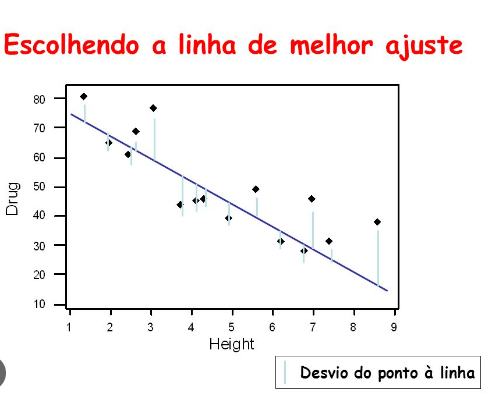
O que raios é a linha de melhor ajuste?

Nosso objetivo principal ao usar a regressão linear é encontrar a famosa “linha de melhor ajuste“.

Isso significa que o erro entre os valores previstos e os valores reais deve ser o menor possível.

Em suma, queremos a menor dor de cabeça com o menor erro possível.

A equação da linha de melhor ajuste nos dá uma linha reta que representa a relação entre as variáveis dependentes e independentes.

A inclinação da linha indica o quanto a variável dependente muda para uma unidade de mudança nas variáveis independentes.

Finalmente, a regressão linear no machine learning

Na regressão linear, nosso trabalho é prever o valor de uma variável dependente (y) com base em uma variável independente (x).

É daí que vem o nome “Regressão Linear”.

Um exemplo clássico, X (entrada) pode ser a experiência de trabalho e Y (saída) é o salário de uma pessoa.

A linha de regressão é a linha de melhor ajuste para o nosso modelo.

A “mágica” da função de custo

Para obter a linha de melhor ajuste, usamos a função de custo para calcular os melhores valores para os coeficientes.

Diferentes valores de pesos ou coeficientes geram diferentes linhas de regressão.

A função de hipótese na regressão linear

Definimos antes que nossa característica independente é a experiência (X) e o salário (Y) é a variável dependente.

Vamos assumir que existe uma relação linear entre X e Y, então o salário pode ser previsto usando:

Y^ = θ1 ​+ θ2​X

OU

yi^​ ​= θ1 ​+ θ2​xi​

Onde,

• yi∈Y(i=1,2,…,n) são os rótulos dos dados (aprendizado supervisionado)
• xi∈X(i=1,2,…,n) são os dados de treinamento independentes (univariados – uma variável de entrada)
• yi^∈Y^(i=1,2,…,n) são os valores previstos.

O modelo obtém a melhor linha de regressão ajustando os melhores valores de θ1e θ2​.

• θ1: intercepto
• θ2: coeficiente de x

Uma vez encontrados os melhores valores para θ1​ e θ2, obtemos a linha de melhor ajuste.

Assim, ao usar nosso modelo para previsão, ele irá prever o valor de y para o valor de entrada x.

Como atualizar os valores de θ1​ e θ2 para obter a linha de melhor ajuste?

Para alcançar a linha de regressão de melhor ajuste, o modelo deve prever o valor alvo Y^ para que o erro entre o valor previsto Y^ e o valor verdadeiro Y seja mínimo.

Portanto, é relevante atualizar os valores de θ1e θ2 para alcançar o melhor valor que minimize o erro entre o valor previsto para y e o valor verdadeiro do y.

minimize 1/n ​∑i=1n ​(yi​^​ − yi​)²

E aí está!

Agora você sabe como encontrar a linha de melhor ajuste na regressão linear.

Aquela que reduz ao mínimo o erro e faz você parecer um gênio dos dados.

Só não esqueça de agradecer ao seu computador por fazer todas as contas chatas por você.

A função de custo para regressão linear

A função de custo, ou função de perda, é o erro ou diferença entre o valor previsto Y^ e o valor real Y.

Na regressão linear, usa-se a famosa função de custo Mean Squared Error (MSE) que calcula a média dos erros quadrados entre os valores previstos yi^ e os valores reais yi.

A ideia é encontrar os valores ideais para o intercepto θ1 e o coeficiente da variável de entrada θ2 que forneçam a linha de melhor ajuste para os pontos de dados.

O cálculo da função MSE é

Cost function(J) = 1/n ​∑ni​(yi​^​−yi​)2

Usando a função MSE, o processo iterativo de descida do gradiente atualiza os valores de θ1​ e θ2​.

Isso garante a convergência do valor de MSE para o mínimo global.

Isso resulta em um ajuste mais preciso da linha de regressão linear ao conjunto de dados.

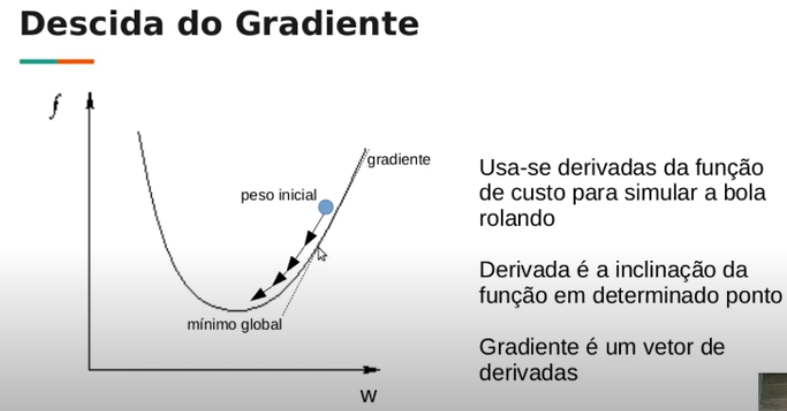
Descendo a ladeira com a descida do gradiente

Para encontrar a linha de melhor ajuste, o modelo deve prever o valor alvo Y^ para que o erro entre o valor previsto Y^ e o valor verdadeiro Y seja o mínimo.

Logo, é preciso atualizar os valores de θ1​ e θ2 para alcançar os melhores valores que minimizem o erro entre o valor previsto para y e o valor verdadeiro de y.

min⁡ 1/n ∑i =1/n (yi^−yi)2

Para isso, usamos a tal da descida do gradiente.

Em suma, é um algoritmo de otimização que ajusta iterativamente os parâmetros do modelo para reduzir o erro quadrático médio (MSE) no conjunto de dados de treinamento.

Começamos com valores aleatórios para θ1 e θ2 e então, passo a passo, ajustamos os valores, movendo em direção ao menor custo.

Diferenciando a função de custo

Para ajustar os coeficientes, precisamos calcular o gradiente da função de custo em relação aos parâmetros θ1​ e θ2.

Diferenciamos a função de custo J em relação a θ1:

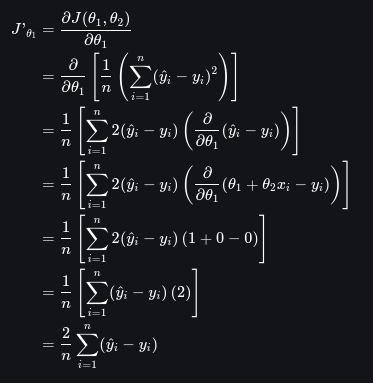
E em relação a θ2​:

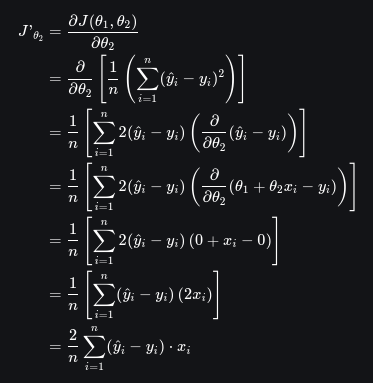
Atualizando os diachos dos parâmetros

Finalmente, ajustamos os parâmetros θ1​ e θ2​ usando uma taxa de aprendizado α:

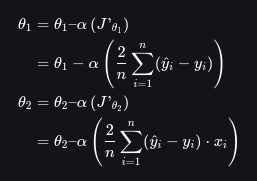
E é assim que ajustamos a linha de regressão linear até que se encaixe certo nos dados.

Um processo aparentemente simples, mas que exige matemática e paciência.

Por isso que muito o chamam de “mágica da descida do gradiente”.

Os pressupostos da regressão linear simples

A regressão linear pode até parecer fácil de entender e de prever o comportamento de uma variável.

Masss, para não ser uma ilusão completa, a regressão tem que se ajustar a alguns pré-requisitos bem menos flexíveis. Vamos aos detalhes:

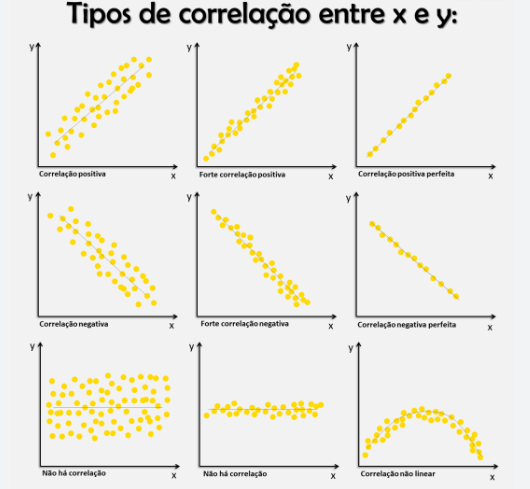
Linearidade

Os dados precisam se comportar como se estivessem em uma linha reta.

A relação entre a variável independente e a dependente tem que ser linear.

Se você não consegue desenhar uma linha reta que passe pela maioria dos pontos, então a regressão linear não vai servir para nada além de enfeitar sua apresentação.

Independência

Cada observação deve ser uma entidade isolada.

O valor de uma observação não deve ter influência alguma sobre o valor de outra.

Se os dados se misturam como numa festa desorganizada, onde todo mundo tem uma influência sobre o outro, então a regressão linear estará mais perdida do que qualquer um nesse evento.

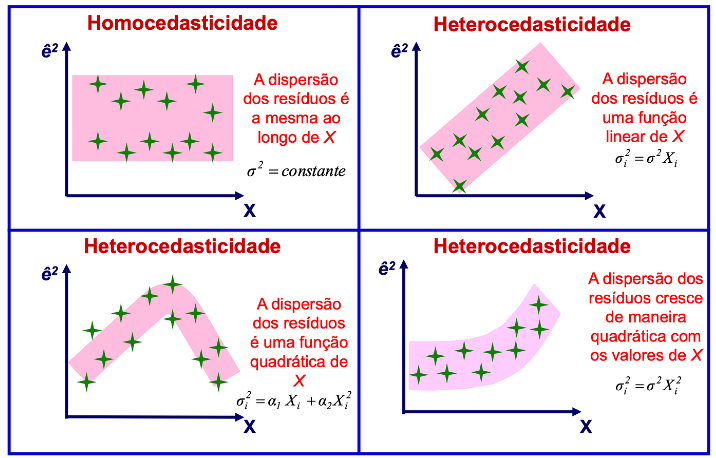
Homoscedasticidade

A variância dos erros tem que ser constante, não importa o nível da variável independente.

Se a variância dos erros parece uma montanha-russa, subindo e descendo sem controle, então sua regressão linear está fazendo água e não vai oferecer um modelo confiável.

Normalidade

Os resíduos (ou erros) precisam seguir a distribuição normal, aquele formato de sino que parece mais um gráfico de vendas bem-sucedidas.

Se seus resíduos estão mais para um carnaval de irregularidades, então a sua regressão linear não vai passar de um truque de mágica tosco.

Resumindo: se a sua análise de regressão linear não consegue se encaixar nesses critérios, você está mais para um ilusionista de dados do que para um cientista.

Os pressupostos da regressão linear múltipla

Para a regressão linear múltipla, você precisa atender aos mesmos quatro pressupostos da regressão linear simples, mas com alguns adicionais para garantir que seu modelo não seja um desastre total. Vamos aos detalhes:

Sem multicolinearidade

Os seus preditores independentes não devem andar de mãos dadas como se fossem melhores amigos.

Não deve haver uma correlação alta entre as variáveis independentes.

Se duas ou mais dessas variáveis estão tão entrelaçadas que é impossível distinguir o impacto individual de cada uma, então sua regressão múltipla está furada.

Aditividade

O modelo assume que o impacto de uma variável preditora sobre a variável resposta é consistente, não importa o que as outras variáveis estejam fazendo.

Isso significa que as variáveis não devem interagir entre si para afetar a variável dependente.

Se houver interações complexas, então sua análise vai ser mais confusa do que uma série de TV cheia de reviravoltas.

Seleção de atributos

Escolher quais variáveis independentes incluir no modelo é crucial.

Se você decidir adicionar variáveis irrelevantes ou redundantes, é como jogar uma quantidade absurda de tempero numa receita: o modelo pode acabar superajustado e se tornar um pesadelo para interpretar.

Overfitting

Overfitting acontece quando seu modelo se ajusta aos dados de treinamento com tanta precisão que acaba capturando ruídos e flutuações aleatórias que não têm nada a ver com a verdadeira relação entre as variáveis.

O resultado?

Seu modelo vai performar mal com novos dados, como se você tivesse feito um trabalho de faculdade e se saído bem apenas porque decorou todas as respostas.

Se a sua regressão múltipla não se encaixa nesses critérios, você está basicamente tentando impressionar com um truque que mais parece um fiasco em potencial.

Multicolinearidade

Multicolinearidade é um fenômeno estatístico irritante que acontece quando duas ou mais variáveis independentes em um modelo de regressão múltipla são tão interligadas que você mal consegue distinguir o impacto individual de cada uma sobre a variável dependente.

É como se você tentasse identificar a contribuição de cada membro em uma banda de rock quando eles todos tocam a mesma nota em uníssono.

A detecção de multicolinearidade usa duas técnicas principais:

Matriz de Correlação

Olhar a matriz de correlação entre as variáveis independentes é uma maneira comum de detectar esse problema.

Se você encontrar correlações altíssimas (perto de 1 ou -1), é um sinal claro de que você pode estar lidando com multicolinearidade.

Se suas variáveis estão se agarrando umas às outras como se fossem parentes próximos, você tem um problema.

VIF (Fator de Inflação da Variância)

O VIF mede o quanto a variância de um coeficiente de regressão estimado aumenta devido à correlação entre os preditores.

Um VIF alto (geralmente acima de 10) é como um alerta vermelho piscando dizendo que a multicolinearidade está em níveis insuportáveis.

Se o VIF for alto, é como se seus preditores estivessem organizando uma competição para ver qual pode inflar mais o erro.

Métricas de Avaliação para Regressão Linear

Para avaliar a força de um modelo de regressão linear, você pode usar uma série de métricas.

Essas avaliações indicam o quão bem o modelo está produzindo os resultados observados.

Se você não checar essas métricas, é como dirigir um carro sem verificar o painel: você pode até chegar ao seu destino, mas não será uma viagem muito segura ou confortável.

Erro Quadrático Médio (EQM)

O Erro Quadrático Médio (EQM) é uma métrica de avaliação que calcula a média dos erros ao quadrado entre os valores reais e os valores previstos para todos os pontos de dados.

Sim, é isso mesmo: você pega a diferença entre o que você previu e o que realmente aconteceu…

Eleva essa diferença ao quadrado (porque só assim erros negativos e positivos não vão se anular) e…

Calcula a média desses erros quadrados.

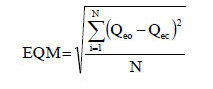
Aqui está o básico:

• N é o número total de pontos de dados.
• Qeo é o valor real ou observado para o i-ésimo ponto de dado.
• Qeo é o valor previsto para o i-ésimo ponto de dado.

EQM é a sua maneira de medir o quão preciso é o modelo nas suas previsões.

Mas tenha em mente que o EQM é extremamente sensível aos outliers.

Ou seja, se houver erros grandes, eles vão fazer o EQM disparar e distorcer o quão bem o modelo realmente está se saindo.

Portanto, se você tem alguns pontos de dados bem fora da curva, eles podem transformar um modelo medíocre em um verdadeiro desastre estatístico.

Erro Absoluto Médio (EAM)

O Erro Absoluto Médio (EAM) é uma métrica de avaliação que mede a precisão de um modelo de regressão de uma forma mais direta do que o EAM. Em vez de elevar ao quadrado as diferenças entre valores previstos e reais, o EAMsimplesmente calcula a média das diferenças absolutas. Em outras palavras, você olha para o erro absoluto (sem se preocupar com o sinal) e calcula a média desses erros.

Aqui está o básico:

• n é o número de observações.
• Y representa os valores reais.
• ŷ são os valores previstos.

Matematicamente, o EAM é expresso como:

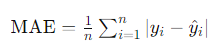
Um valor mais baixo de EAM indica que o modelo está indo bem. E, ao contrário do EQM, o EAM não se deixa arrastar por outliers porque considera apenas diferenças absolutas, sem se importar com a direção do erro.

Portanto, se você quer uma métrica que não fique obcecada por erros extremos, o EAM é o caminho a seguir.

Erro Quadrático Médio (EQM)

Erro Quadrático Médio (EQM ou RMSE em inglês) é a raiz quadrada da variância dos resíduos.

Isso nos diz o quão bem os pontos de dados observados se encaixam nos valores esperados.

Ou seja, quão bem o modelo está ajustado aos dados.

É como se estivéssemos medindo a precisão do nosso modelo, mas sem muitas expectativas.

Na notação matemática, é expresso da seguinte maneira:

Em vez de dividir o número total de pontos de dados pelo número de graus de liberdade, é preciso dividir a soma dos resíduos quadrados para obter uma estimativa não tendenciosa.

Essa estimativa é conhecida como Erro Padrão dos Resíduos (EPR).

Na notação matemática, é expresso assim:

Mas, sejamos francos: o EQM não é lá grande coisa em comparação com o R-quadrado.

O EQM pode variar dependendo das unidades das variáveis, pois seu valor depende diretamente das unidades das variáveis.

Ou seja, o EQM não é uma medida normalizada.

O EQM é sensível ao tipo de dados que você está usando.

O EQM não é exatamente a métrica mais confiável para comparar modelos, em especial se as variáveis tiverem unidades diferentes.

Coeficiente de Determinação (R-quadrado)

O R-quadrado é um número que tenta mostrar o quanto o modelo que você desenvolveu consegue explicar ou capturar a variação dos dados.

Sempre fica entre 0 e 1.

Em teoria, quanto maior o R-quadrado, melhor o modelo está encaixando nos dados.

É uma forma elegante de dizer: “Olha, eu sou bom, confie em mim!”

Na notação matemática, é expresso assim:

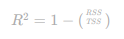
Soma dos Quadrados dos Resíduos (RSS)

Isso é a soma dos quadrados das diferenças entre o que você observou e o que esperava.

É o quanto o modelo erra, ponto por ponto.

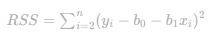
Soma Total dos Quadrados (TSS)

Aqui, você soma os erros de cada ponto de dados em relação à média da variável dependente.

É o quanto, em média, os dados estão longe da média esperada.

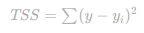
O R-quadrado mede a proporção da variação na variável dependente que é explicada pelas variáveis independentes no modelo.

É uma tentativa de mostrar o quão bem o modelo consegue explicar o que está acontecendo com os dados.

No entanto, lembre-se: um R-quadrado alto não significa que seu modelo é perfeito…

Significa apenas que ele é melhor do que nada.

Não se esqueça de usar outras métricas para obter uma visão mais completa.

Erro do R-quadrado ajustado

O R-quadrado ajustado é um truque para mostrar a proporção da variação na variável dependente que as variáveis independentes conseguem explicar em um modelo de regressão.

Mas, ao contrário do R-quadrado comum, o R-quadrado ajustado é mais esperto.

Ele leva em conta o número de previsores no modelo e dá uma rasteira nos modelos que tentam impressionar ao incluir variáveis irrelevantes que não ajudam em nada a explicar a variação na variável dependente.

Na notação matemática, o R-quadrado ajustado é expresso assim:

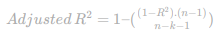
Aqui,

• n é o número de observações
• k é o número de previsores no modelo
• R é o coeficiente de determinação

O R-quadrado ajustado é o herói que evita o sobreajuste.

Ele dá uma bronca no modelo que tenta parecer mais sofisticado do que realmente é ao adicionar previsores que não fazem diferença significativa na explicação da variável dependente.

O R-quadrado ajustado garante que seu modelo não esteja simplesmente se enchendo de variáveis para enganar o sistema e parecer mais “inteligente” do que realmente é.

Implementando regressão linear com Python

Importe as bibliotecas abaixo:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.axes as ax
from matplotlib.animation import FuncAnimation

Dê carga no dataset e separe as variáveis de entrada e as variáveis alvo.

O dataset está neste link.

url = ‘https://media.geeksforgeeks.org/wpcontent/uploads/20240320114716/data_for_lr.csv’
data = pd.read_csv(url)
data
# Retirando os valores que estão faltando
data = data.dropna()
# Treinando o dataset e os classificadores (labels)
train_input = np.array(data.x[0:500]).reshape(500, 1)
train_output = np.array(data.y[0:500]).reshape(500, 1)
# Validando o dataset e os classificadores (labels)
test_input = np.array(data.x[500:700]).reshape(199, 1)
test_output = np.array(data.y[500:700]).reshape(199, 1)

Construa o modelo de regressão linear e plote a linha de regressão…

Siga os seguintes passos…

Propagação para frente

Comece aplicando a função de regressão linear Y=mx+c, onde m e c são inicialmente atribuídos com valores aleatórios.

Isso é como começar uma receita de bolo sem saber se os ingredientes são os certos.

Função de custo

Em seguida, você precisa calcular a função de custo, que é a média dos erros entre os valores previstos e os valores reais.

É como checar se o bolo ficou bom ou não.

Quanto menor o custo, melhor a receita.

Em resumo, você está ajustando a receita (modelo) e verificando o quão bem ela se sai.

Depois, você plota a linha de regressão para ver como o modelo se ajusta aos dados reais.

class LinearRegression:
def __init__(self):
self.parameters = {}
def forward_propagation(self, train_input):
m = self.parameters['m']
c = self.parameters['c']
predictions = np.multiply(m, train_input) + c
return predictions
def cost_function(self, predictions, train_output):
cost = np.mean((train_output - predictions) ** 2)
return cost
def backward_propagation(self, train_input, train_output,
predictions):
derivatives = {}
df = (predictions-train_output)
# dm= 2/n * media de (predictions-actual) * input
dm = 2 * np.mean(np.multiply(train_input, df))
# dc = 2/n * media de (predictions-actual)
dc = 2 * np.mean(df)
derivatives['dm'] = dm
derivatives['dc'] = dc
return derivatives
def update_parameters(self, derivatives, learning_rate):
self.parameters['m'] = self.parameters['m'] -
learning_rate * derivatives['dm']
self.parameters['c'] = self.parameters['c'] -
learning_rate * derivatives['dc']
def train(self, train_input, train_output, learning_rate,
iters):
# Inicializando os parâmetros aleatórios
self.parameters['m'] = np.random.uniform(0, 1) * -1
self.parameters['c'] = np.random.uniform(0, 1) * -1
# Inicializando as perdas
self.loss = []
# Inicializando as figuras e os eixos para animação
fig, ax = plt.subplots()
x_vals = np.linspace(min(train_input), max(train_input),
100)
line, = ax.plot(x_vals, self.parameters['m'] * x_vals +
self.parameters['c'], color='red', label='Regression Line')
ax.scatter(train_input, train_output, marker='o', color='green', label='Training Data')
# Setando os limites do eixo y para excluir valores negativos
ax.set_ylim(0, max(train_output) + 1)
def update(frame):
# Propagação para frente 
predictions = self.forward_propagation(train_input)
# Função de custo
cost = self.cost_function(predictions, train_output)
# Propagação para trás
derivatives = self.backward_propagation(train_input, train_output, predictions)
# Atualizando os parâmetros 
self.update_parameters(derivatives, learning_rate)
# Atualizando a linha de regressão 
line.set_ydata(self.parameters['m'] * x_vals + self.parameters['c'])
# Adicionando as perdas e imprimindo
self.loss.append(cost)
print("Iteration = {}, Loss = {}".format(frame + 1, cost))
return line,
# Criando a animação
ani = FuncAnimation(fig, update, frames=iters, interval=200, blit=True)
# Salvando a animação como um arquivo de vídeo
ani.save('linear_regression_A.gif', writer='ffmpeg')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Linear Regression')
plt.legend()
plt.show()
return self.parameters, self.loss

Agora veja o modelo treinado já com as predições e estimativas.

#Exemplo de utilização
linear_reg = LinearRegression()
parameters, loss = linear_reg.train(train_input, train_output, 0.0001, 20)

Output:
Iteration = 1, Loss = 9130.407560462196
Iteration = 1, Loss = 1107.1996742908998
Iteration = 1, Loss = 140.31580932842422
Iteration = 1, Loss = 23.795780526084116
Iteration = 2, Loss = 9.753848205147605
Iteration = 3, Loss = 8.061641745006835
Iteration = 4, Loss = 7.8577116490914864
Iteration = 5, Loss = 7.8331350515579015
Iteration = 6, Loss = 7.830172502503967
Iteration = 7, Loss = 7.829814681591015
Iteration = 8, Loss = 7.829770758846183
Iteration = 9, Loss = 7.829764664327399
Iteration = 10, Loss = 7.829763128602258
Iteration = 11, Loss = 7.829762142342088
Iteration = 12, Loss = 7.829761222379141
Iteration = 13, Loss = 7.829760310486438
Iteration = 14, Loss = 7.829759399646989
Iteration = 15, Loss = 7.829758489015161
Iteration = 16, Loss = 7.829757578489033
Iteration = 17, Loss = 7.829756668056319
Iteration = 18, Loss = 7.829755757715535
Iteration = 19, Loss = 7.829754847466484
Iteration = 20, Loss = 7.829753937309139

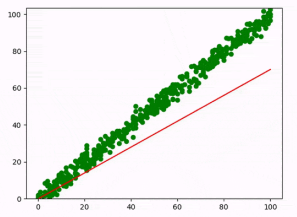
A tal da linha de regressão linear

A linha de regressão linear é como aquele amigo doido que tenta te dar conselhos sobre relacionamentos.

Ele pode até ter boas intenções, mas nem sempre acerta.

Essa linha mostra a relação entre duas variáveis e representa a melhor linha possível para capturar a tendência geral de como a variável dependente (Y) muda em resposta às variações na variável independente (X).

A linha de regressão linear positiva

Se a linha de regressão é positiva, isso significa que há uma relação direta entre a variável independente (X) e a variável dependente (Y).

Quanto mais X cresce, mais Y cresce também.

A inclinação da linha é positiva, o que quer dizer que ela sobe da esquerda para a direita.

É como aquele momento em que você percebe que, quanto mais você estuda, melhor suas notas ficam (pelo menos na teoria).

A linha de regressão linear negativa

Se a linha de regressão é negativa, indica uma relação inversa entre X e Y.

Conforme X aumenta, Y diminui.

A inclinação da linha é negativa, significando que ela desce da esquerda para a direita.

É como se você tentasse economizar dinheiro e, quanto mais você tenta, mais suas despesas aumentam.

A linha de regressão linear é sua tentativa de mostrar como uma variável afeta a outra.

Mas lembre-se, ela é apenas uma simplificação e não deve ser vista como uma verdade absoluta.

Técnicas de Regularização para Modelos Lineares

Aqui estão algumas técnicas de regularização para modelos lineares para que eles fiquem mais próximos da realidade…

Regressão Lasso (Regularização L1)

O Lasso é a técnica que tenta colocar um freio no modelo de regressão linear, adicionando um termo de penalização.

É tipo um aviso para o modelo não se empolgar e começar a fazer previsões absurdas.

A função objetivo, após aplicar o Lasso, é:

O primeiro termo é a perda de mínimos quadrados que é a diferença quadrada entre os valores previstos e reais.

O segundo termo é a regularização L1 que penaliza a soma dos valores absolutos dos coeficientes de regressão θ.

É um jeito elegante de dizer: “Pare de se vangloriar e mantenha os coeficientes sob controle.”

Regressão Ridge (Regularização L2)

A regressão Ridge é outra forma de regularizar a regressão linear, mas desta vez a penalização é um pouco diferente.

Aqui, o objetivo é impedir que os coeficientes se tornem gigantescos e estraguem tudo.

A função objetivo após aplicar a Ridge é:

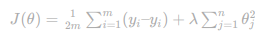
O primeiro termo é a perda de mínimos quadrados, como antes, e o segundo termo é a regularização L2 que penaliza a soma dos quadrados dos coeficientes de regressão θ.

Ideal quando seus preditores estão mais correlacionados do que amigos de redes sociais—ou seja, quando há multicolinearidade.

Regressão Elastic Net

A regressão Elastic Net é tipo uma mistura das regressões Lasso e Ridge.

Se você não consegue decidir qual regularização usar, o Elastic Net faz a escolha por você, combinando L1 e L2.

A função objetivo inclui:

A perda de mínimos quadrados (primeiro termo), a regularização L1 (segundo termo) e a regularização L2 (terceiro termo).

O parâmetro α controla a mistura entre L1 e L2 para que você possa ter o melhor dos dois mundos sem precisar ficar indeciso.

Resumindo, essas técnicas ajudam seu modelo a não exagerar e a se comportar de maneira mais sensata.

Isso evita que ele se torne um modelo exagerado que faz previsões baseadas em qualquer pequeno detalhe dos dados.

As aplicações ‘reais’ da regressão linear

Regressão linear, a ferramenta adorada por tantos profissionais que se acham experts em tudo, de finanças até a psicologia.

A regressão linear serve para tentar prever o comportamento de variáveis específicas…

Como se os números fossem mágicos e pudessem revelar todos os segredos do universo financeiro e psicológico.

No mundo das finanças, essa técnica serve para analisar a relação entre o preço das ações de uma empresa e seus lucros, ou para tentar adivinhar o valor futuro de uma moeda com base no seu desempenho passado.

E claro, como se previsões baseadas em tendências passadas fossem infalíveis…

As vantagens de uma regressão linear

A regressão linear é um método simples que parece mais um truque de mágica do que uma ciência.

Para começar, é fácil de entender e implementar já que ninguém gosta de complicação quando se trata de estatística.

Os coeficientes do modelo de regressão linear mostram como a variável dependente muda com uma alteração unitária na variável independente.

É como se dissesse: “Olhe, aqui está o impacto de um pequeno empurrãozinho.”

E não se esqueça da eficiência computacional!

Regressão linear lida com grandes conjuntos de dados como um campeão, processando-os rapidamente e se tornando ideal para aquelas aplicações em tempo real que todos adoram.

A regressão é relativamente resistente a valores discrepantes – pelo menos mais do que muitos algoritmos de aprendizado de máquina sensíveis a qualquer mudança mínima nas variáveis.

A regressão linear costuma ser um modelo básico decente para comparar com aquelas técnicas mais sofisticadas e misteriosas.

A regressão tem um histórico glorioso e disponível em quase todas as bibliotecas e pacotes de software de aprendizado de máquina por aí.

Agora, as desvantagens da regressão linear

A regressão linear é o velho truque que nem sempre faz o truque.

Uma das suas falhas mais notórias é assumir que a relação entre a variável dependente e as independentes é linear.

Se essa relação não for tão retinha assim, prepare-se para um desempenho tosco.

Não podemos nos esquecer da sensibilidade à multicolinearidade…

Aquele problema chato que acontece quando as variáveis independentes estão tão grudadas que parece que são uma grande família.

Isso pode inflar a variância dos coeficientes e deixar as previsões do modelo mais instáveis do que um castelo de cartas.

Outra maravilha da regressão linear é que ela espera que suas características (ou features) já estejam no formato perfeito.

Ou seja, você pode ter que fazer um trabalho extra, transformando essas características para que o modelo não fique completamente perdido.

Além disso, a regressão linear é um campo de batalha entre overfitting e underfitting.

Overfitting é quando o modelo aprende a treinar os dados tão bem que não consegue lidar com dados novos.

É tipo decorar um roteiro e se perder no palco.

Já o underfitting é quando o modelo é tão simplista que não consegue capturar as complexidades do data.

É que nem o caso do aluno que não estuda o suficiente.

Por último, a regressão linear tem um poder explicativo limitado para as relações mais complexas entre variáveis.

Conclusões realistas

A regressão linear é o básico do básico para o aprendizado de máquina.

Ela é aquele algoritmo fundamental que todo mundo usa porque é simples, fácil de entender e, às vezes, eficiente.

Serve para decifrar relações entre variáveis e fazer previsões em diversos contextos.

Mas, a regressão linear também tem suas limitações.

Ela vive no mundo das suposições de linearidade e é sensível à multicolinearidade…

Duas fragilidades que podem transformar um modelo promissor em um desastre total.

A regressão linear pode ser uma ferramenta boa para análise de dados e previsão.

Só não espere que ela faça milagres quando as coisas ficam realmente complicadas…

Pedro Londe

Palestrante e autor do livro “O que diabos é Gig Economy?: Como ter várias fontes de renda e aproveitar ao máximo todas as suas habilidades”